Quantum teleportation is a groundbreaking technique in quantum information science that enables the transfer of a quantum state from one particle to another, without moving the particle itself. Despite its sci-fi-sounding name, it’s not about teleporting matter or people, but transmitting the exact information that defines a quantum state. This tutorial explains every term in simple language, provides illustrative examples and offer learn quantum teleportation in simple way with examples.

What is Quantum Teleportation?

Quantum teleportation transfers the full information describing a quantum state from one qubit (quantum bit) held by Alice to another qubit held by Bob, using an entangled pair and classical communication. The original state at Alice is destroyed, preserving quantum no-cloning rules.

Why No-Cloning Matters?

The no-cloning theorem says an unknown quantum state cannot be copied perfectly, so direct duplication is impossible and measurement disturbs the state. Teleportation solves this by performing a destructive joint measurement and using classical bits to apply a corrective operation on an entangled partner, recreating the original state elsewhere.

Key Concepts Explained

Quantum State

A quantum state describes all the information about a quantum system, like the orientation of a qubit on the Bloch sphere. It can be written as α∣0⟩+β∣1⟩α∣0⟩+β∣1⟩, where α and β are complex amplitudes satisfying ∣α∣2+∣β∣2=1∣α∣2+∣β∣2=1.

Qubit

A qubit is the quantum analogue of a classical bit. Unlike a classical bit, which is either 0 or 1, a qubit can exist in a superposition of both states simultaneously.

Entanglement

Entanglement is a quantum correlation between particles. An entangled pair’s combined state can’t be described individually. For example, an entangled Bell state:

|Ψ^+⟩ = (1/√2)(|00⟩ + |11⟩)

How Does Quantum Teleportation Work?

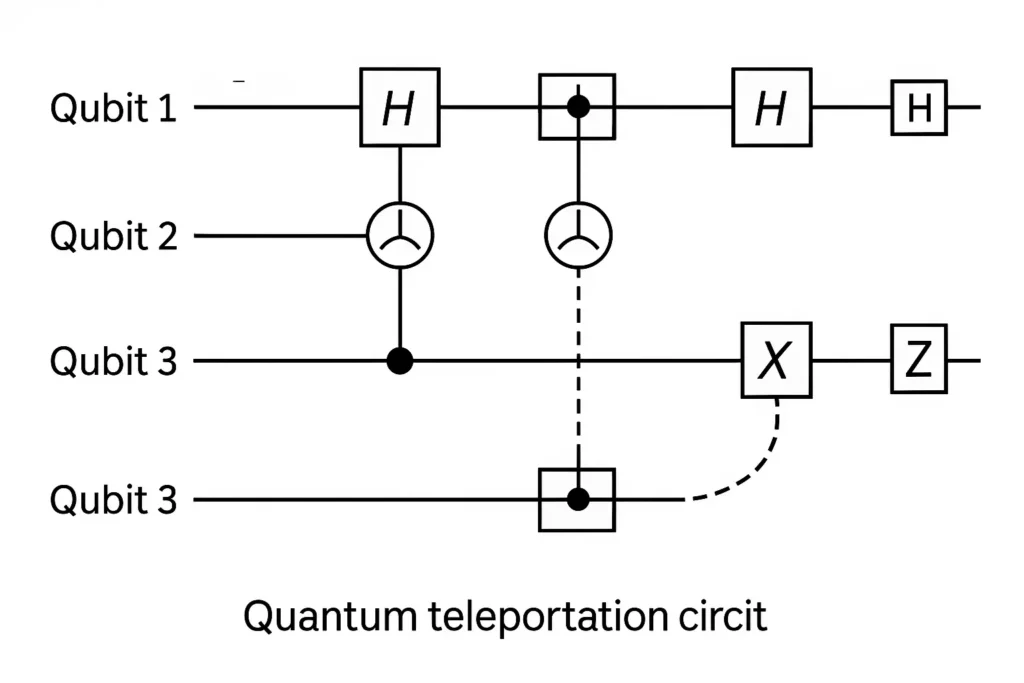
Preparation: Entangling Qubits

Alice and Bob share an entangled qubit pair. Alice holds qubit A (the state to teleport) and qubit E, Bob holds qubit B entangled with E.

Bell-State Measurement

Alice performs a Bell-state measurement on qubits A and E, projecting them into one of four Bell states. This collapses Bob’s qubit B into a corresponding state related to A’s original state.

Classical Communication

Alice sends Bob two classical bits indicating which Bell state was measured.

Reconstruction of the State

Bob applies one of four unitary operations (identity, X, Z, or XZ) to qubit B based on Alice’s bits. This transforms B into the original state α∣0⟩+β∣1⟩.

A Simple Example

Suppose Alice’s qubit A is in the state |Ψ⟩ = (1/√2)(|0⟩ + |1⟩). After sharing entanglement and following the protocol, Bob’s qubit B ends up in the same superposition, even though A was never physically sent.

Real Experiments and Records

Teleportation over optical fiber has reached 100 km, showing feasibility for long-distance quantum communication over installed infrastructure. Satellite experiments (e.g., Micius/QUESS) extended entanglement distribution to about 1,200 km in free space, a key step toward global quantum networks.

Hands-on: Minimal Circuit Idea

A minimal three-qubit demo prepares an unknown message qubit, entangles two others (Alice–Bob), performs a Bell measurement on Alice’s pair, sends two classical bits, and applies X/Z corrections on Bob’s qubit to recover the message state; this is commonly implemented in OpenQASM tutorials and simulators. Such tutorials show the exact gate sequence (Hadamard, CNOT, Bell measurement, conditional Pauli corrections) for learning and experimentation.

Applications and Future Directions

• Quantum Networks: Building secure quantum internet links.
• Quantum Computing: Transferring states between quantum processors.
• Quantum Cryptography: Enhancing quantum key distribution.

Researchers aim to teleport states over longer distances and integrate teleportation into large-scale quantum architectures.

References:

• Nielsen & Chuang, Quantum Computation and Quantum Information (https://doi.org/10.1017/CBO9780511976667)
• IBM Quantum: Quantum Teleportation Tutorial (https://quantum-computing.ibm.com/docs/)
• QuTech Academy: Quantum Teleportation Lecture (https://qutech.nl/academy)