Bell’s Theorem stands as one of the most groundbreaking discoveries in modern physics, fundamentally challenging our understanding of reality itself. This remarkable theorem, introduced by physicist John Stewart Bell in 1964, demonstrates that no local hidden-variable theory can reproduce the predictions of quantum mechanics. The implications are profound: our universe operates in ways that defy classical intuition, where particles can influence each other instantaneously across vast distances through a phenomenon Einstein famously called “spooky action at a distance”

What is Bell’s Theorem? Understanding the Fundamentals

Bell’s Theorem is a collection of mathematical results that prove quantum mechanics is fundamentally incompatible with local hidden-variable theories. To understand this revolutionary concept, we need to break down its key components.

Hidden variables are theoretical properties of quantum particles that classical physics assumes must exist, even if we cannot observe them directly. Think of it like a coin that already “knows” whether it will land heads or tails before you flip it, even though you cannot see this predetermined outcome.

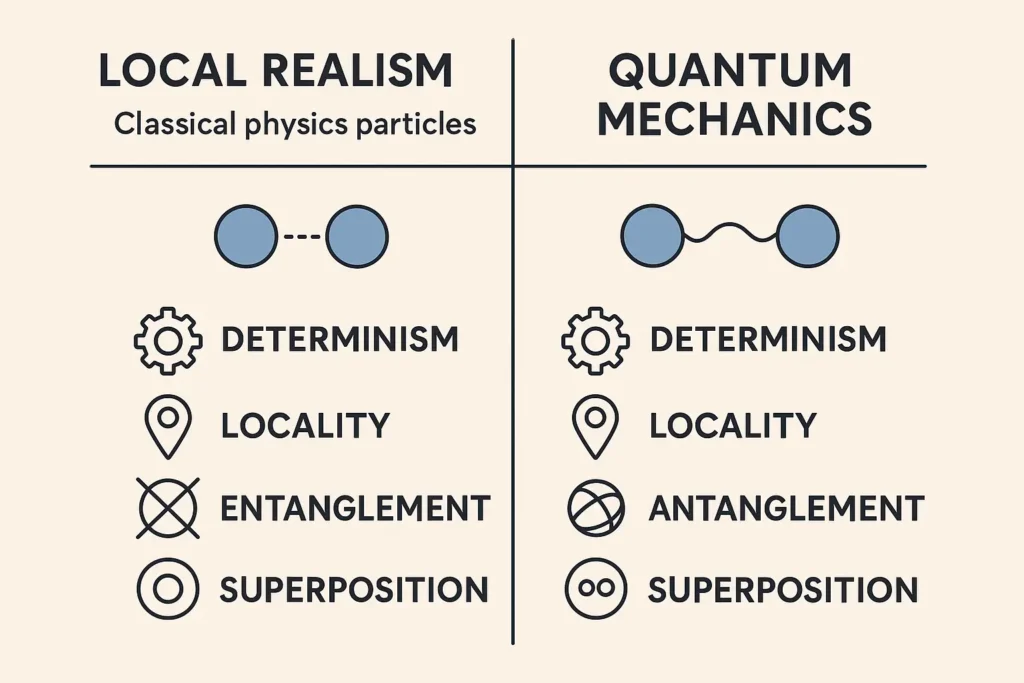
Local realism combines two classical assumptions about our universe. Locality means that objects can only be influenced by their immediate surroundings, with no instantaneous effects across distances or No one can travel beyond the speed of light. Realism assumes that physical properties exist independently of observation.

Bell’s groundbreaking insight was proving that if quantum mechanics is correct, then our world cannot be both local and realistic. This means either particles can influence each other faster than light (violating locality), or physical properties do not exist until measured (violating realism)

The Core Concept Explained Simply

Imagine two magic coins that are created together and then separated by vast distances. In classical physics, each coin would have a predetermined outcome – heads or tails – that exists even before you flip it. However, Bell’s Theorem shows that quantum particles behave differently.

When you measure one quantum particle, it instantly affects its “partner” particle, no matter how far apart they are. This connection is so strong that measuring one particle immediately determines the properties of the other. This phenomenon, called quantum entanglement, cannot be explained by any classical theory.

The Einstein-Podolsky-Rosen (EPR) Paradox: Setting the Stage

The story of Bell’s Theorem begins with a famous thought experiment proposed by Albert Einstein, Boris Podolsky, and Nathan Rosen in 1935, known as the EPR Paradox. Einstein was deeply troubled by quantum mechanics’ implications and sought to prove the theory was incomplete.

Einstein believed that “God does not play dice with the universe” and that physical reality must be deterministic. The EPR Paradox argued that if quantum mechanics were complete, it would require “spooky action at a distance” – instantaneous influences between separated particles.

The EPR team proposed that quantum mechanics must be missing something – hidden variables that would restore classical determinism to physics. They argued that these hidden variables would eliminate the apparent randomness and mysterious connections predicted by quantum theory.

Einstein’s Opposition to Quantum Mechanics

Einstein’s main objections to quantum mechanics centered on three key issues:

1. Randomness: Quantum mechanics suggests that some events are truly random, not just unpredictable due to our ignorance
2. Non-locality: Entangled particles seem to communicate instantaneously, violating the speed of light limit
3. Observer effect: The act of measurement appears to fundamentally change reality

These objections led Einstein to famously state that quantum mechanics must be incomplete and that there must be hidden variables governing particle behavior.

Local Realism vs Quantum Mechanics: The Great Debate

The debate between Einstein and quantum mechanics pioneers like Niels Bohr represented two fundamentally different worldviews about the nature of reality.

Classical Physics Worldview (Local Realism)

Classical physics, as developed by Newton and refined by Einstein’s relativity, operates under several key assumptions:

• Determinism: Complete knowledge of a system’s current state allows perfect prediction of its future
• Locality: Objects are only influenced by their immediate surroundings
• Realism: Physical properties exist independently of observation
• Causality: Effects cannot occur before their causes

Under this worldview, particles have definite properties at all times, even when not being measured. Correlations between distant particles must result from their shared history when they were together, not from ongoing communication.

Quantum Mechanics Worldview

Quantum mechanics presents a radically different picture of reality:

• Probabilistic: Even with complete information, we can only predict probabilities
• Non-local: Measurement of one particle instantly affects distant entangled partners
• Observer-dependent: Properties may not exist until measured
• Wave-particle duality: Particles exhibit both wave and particle characteristics

In the quantum world, particles can exist in multiple states simultaneously until measured, a property called superposition. When entangled particles are separated, they remain connected through what Einstein called “spooky action at a distance”

Bell’s Inequality: The Mathematical Framework

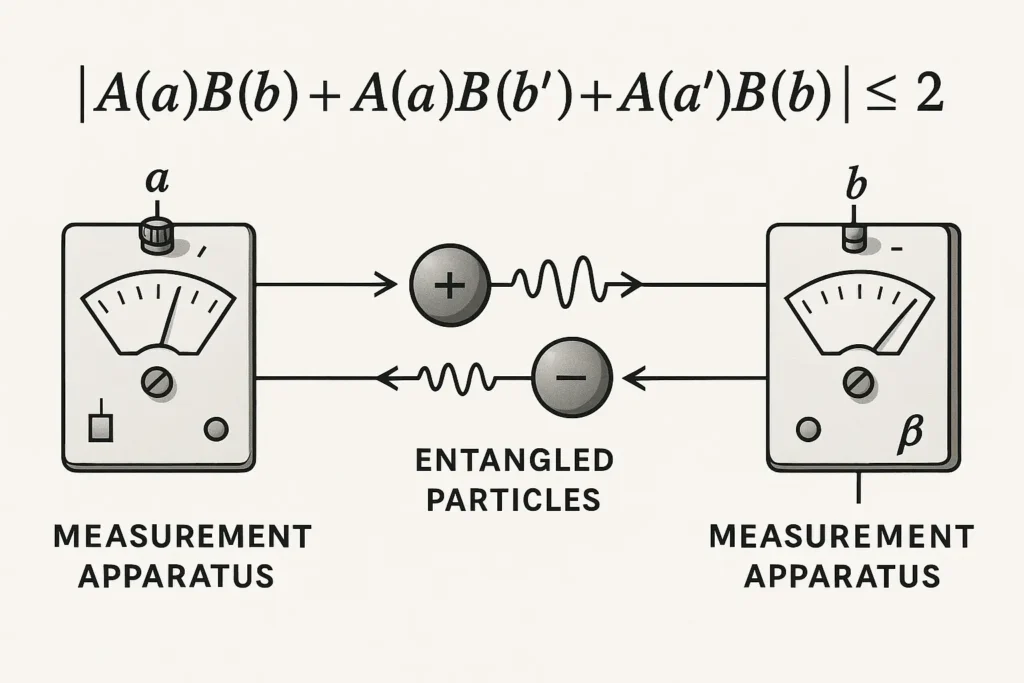
John Stewart Bell’s brilliant contribution was developing a mathematical test that could distinguish between classical and quantum predictions. Bell derived mathematical inequalities that must be satisfied if local realism is correct.

The CHSH Inequality

The most commonly used form of Bell’s inequality is the Clauser-Horne-Shimony-Holt (CHSH) inequality:

|E(a,b) – E(a,b’) + E(a’,b) + E(a’,b’)| ≤ 2

Where E(a,b) represents the correlation between measurements made at different settings. If local hidden variables exist, this inequality cannot be violated.

Quantum Mechanical Predictions

Quantum mechanics predicts correlations that can violate Bell’s inequality, reaching values up to 2√2 ≈ 2.828. This violation occurs when particles are in maximally entangled states.

The key insight is that if experimental results violate Bell’s inequality, then local realism must be false. No classical theory based on predetermined particle properties can explain such strong correlations.

Simple Example: The Photon Polarization Experiment

Consider two entangled photons sent in opposite directions to Alice and Bob. Each person can measure their photon’s polarization along one of three angles: 0°, 120°, or 240°.

Classical physics predicts that Alice and Bob will get the same result at most 67% of the time when measuring along different angles. However, quantum mechanics predicts they will agree 75% of the time – a clear violation of Bell’s inequality.

Real-World Applications of Bell’s Theorem

Bell’s Theorem is not just a philosophical curiosity – it has enabled revolutionary technologies that are transforming our world.

Quantum Computing

Quantum computers rely fundamentally on quantum entanglement to perform calculations impossible for classical computers. By manipulating entangled quantum bits (qubits), quantum computers can solve certain problems exponentially faster.

Applications include:

• Cryptography breaking: Quantum computers could crack current encryption methods
• Drug discovery: Modeling molecular interactions for pharmaceutical research
• Financial modeling: Optimizing complex trading strategies

Quantum Cryptography

Bell’s Theorem enables quantum key distribution, providing theoretically unbreakable encryption. Any attempt to intercept quantum-encrypted messages necessarily disturbs the quantum state, alerting the communicating parties.

Medical Technology

Many medical technologies depend on quantum mechanical principles:

• MRI scanners use quantum spin properties to image inside the human body
• PET scanners detect quantum entanglement in positron-electron annihilation
• Laser surgery employs quantum light emission processes

GPS and Navigation

Atomic clocks in GPS satellites rely on quantum mechanical precision to maintain the accuracy needed for navigation. Without quantum mechanics, GPS would accumulate errors of several kilometers per day.

Nobel Prize Recognition and Modern Experiments

The 2022 Nobel Prize in Physics was awarded to Alain Aspect, John Clauser, and Anton Zeilinger for their groundbreaking experiments testing Bell’s theorem.

John Clauser’s Pioneer Work

John Clauser conducted the first experimental test of Bell’s inequality in 1972. His results clearly violated the inequality, supporting quantum mechanics over local realism. However, early experiments had potential loopholes that could allow classical explanations.

Alain Aspect’s Refinements

Alain Aspect improved upon Clauser’s work by developing methods to change measurement settings after the photons had already been emitted. This eliminated the possibility that measurement settings could influence the particle creation process.

Anton Zeilinger’s Advanced Studies

Anton Zeilinger pioneered quantum teleportation and created increasingly complex entangled states, including entanglement of up to ten photons. His work has enabled practical quantum information technologies.

Modern Loophole-Free Experiments

The most convincing Bell tests have been performed only recently. Loophole-free experiments conducted since 2015 have closed all potential classical explanations:

• Detection loophole: Ensured high-efficiency detection of all particles
• Locality loophole: Guaranteed measurement settings were changed faster than light could travel between detectors
• Freedom-of-choice loophole: Used random number generators to select measurement settings

Why Bell’s Theorem Matters Today

Bell’s Theorem represents more than just an abstract physics principle – it fundamentally challenges our understanding of reality and enables transformative technologies.

Philosophical Implications

Bell’s Theorem forces us to abandon at least one cherished classical assumption:

• Either locality is false: Particles can influence each other faster than light
• Or realism is false: Physical properties do not exist until measured
• Or both: Our classical intuitions about reality are fundamentally wrong

Most physicists accept that the universe is fundamentally non-local, with quantum entanglement representing a real feature of nature rather than a limitation of our knowledge.

Technological Revolution

The technologies enabled by Bell’s Theorem are revolutionizing multiple fields:

Quantum Internet: Networks of entangled particles could enable ultra-secure communication and distributed quantum computing. Research groups worldwide are developing quantum repeaters and quantum memory devices.

Quantum Sensing: Entangled particles can measure physical quantities with unprecedented precision. Applications include detecting gravitational waves, magnetic fields, and chemical concentrations.

Quantum Simulation: Controlled quantum systems can simulate complex materials and biological processes that are impossible to model classically. This could revolutionize drug discovery and materials science.

Future Implications

Bell’s Theorem continues to inspire new research directions:

• Quantum machine learning: Using quantum entanglement to enhance artificial intelligence
• Quantum biology: Understanding how quantum effects influence biological processes
• Fundamental physics: Exploring the connections between quantum mechanics and gravity

Educational Impact

Understanding Bell’s Theorem is crucial for anyone interested in modern science and technology. It demonstrates how theoretical physics discoveries can lead to practical applications that transform society.

The theorem also illustrates the importance of questioning fundamental assumptions about reality. Just as Bell challenged Einstein’s classical worldview, future discoveries may overturn our current understanding of quantum mechanics.

Conclusion

Bell’s Theorem stands as one of the most profound discoveries in physics, demonstrating that our universe operates according to fundamentally non-classical principles. By proving that no local hidden-variable theory can explain quantum mechanical predictions, Bell forever changed our understanding of reality itself.

The experimental verification of Bell’s Theorem has not only settled a decades-long debate about the nature of quantum mechanics but has also enabled revolutionary technologies that are reshaping our world. From quantum computers to unbreakable encryption, the practical applications of Bell’s insights continue to multiply.

As we stand on the threshold of the quantum age, Bell’s Theorem reminds us that the universe is far stranger and more wonderful than our classical intuitions suggest. The “spooky action at a distance” that Einstein rejected has become the foundation for technologies that will define the 21st century.

Understanding Bell’s Theorem is essential for anyone seeking to grasp the modern scientific worldview and the quantum technologies that will shape our future. It represents not just a triumph of theoretical physics, but a testament to the power of bold thinking to reveal the deepest secrets of reality.